Spirograph Flower 

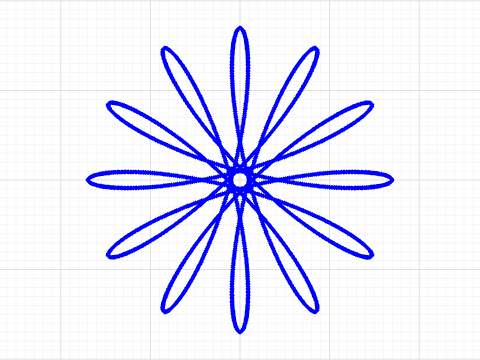
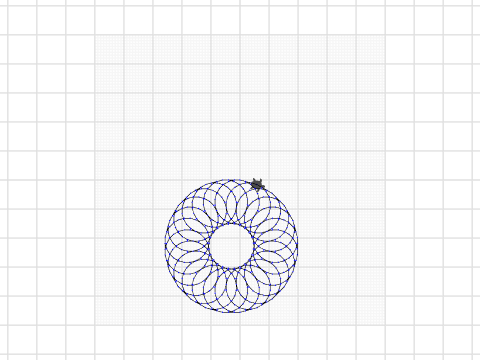
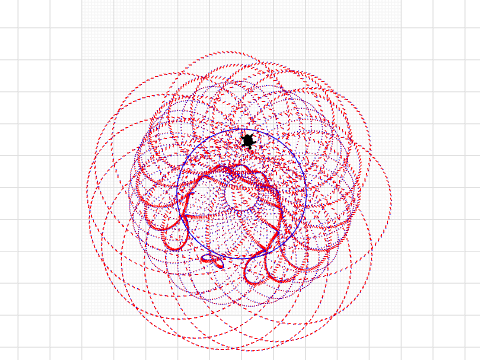
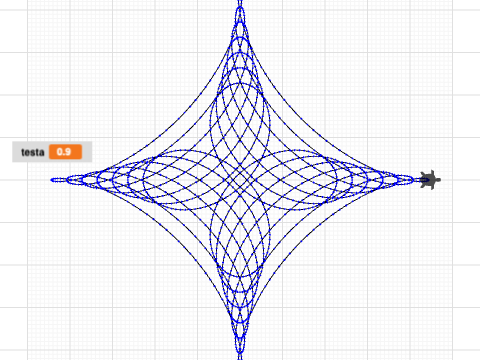
This program recreates the classic Spirograph, a geometric drawing toy invented by British engineer Denys Fisher in 1965. Like the original, it uses two wheels—a fixed outer ring (R=96 or 105) and a rotating inner wheel (r)—to create intricate mathematical curves called hypotrochoids.
The program uses parametric equations to calculate each point on the curve:

x = (R - r) × cos(angle) + p × r × cos((R - r)/r × angle)
y = (R - r) × sin(angle) - p × r × sin((R - r)/r × angle)

The big wheel has either 96 or 105 teeth, while the small wheel can have 24, 30, 32, 36, 40, 42, 45, 48, 50, 52, 56, 60, 63, 64, 72, 75, 80, or 84 teeth. The 'p' variable represents the pen position as a fraction of r (the small wheel's radius). The program completes the pattern by iterating through (r / GCD(R, r)) × 360 degrees—dividing the small wheel size by the greatest common divisor of both wheels, then multiplying by 360—which determines exactly how many degrees the small wheel must rotate for the pattern to close perfectly.